Cho S : x 2 + y 2 + z 2 = 3 và d : x - 1 2 = y + 1 - 2 = z - 1 . Biết d ∩ S = E , F . Tính EF.
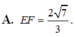
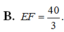
![]()

Cho x,y,z thỏa mãn x,y,z khác 0 và x+y+z=0. Tính
S=1/x^2+y^2-z^2+1/y^2+z^2-x^2+1/z^2+x^2-y^2
\(x+y+z=0\)
⇔\(-x=y+z\)
⇔\(x^2=\left(y+z\right)^2\)
⇔\(x^2=y^2+2yz+z^2\)
⇔\(y^2+z^2-x^2=-2yz\)
Tương tự:
\(z^2+x^2-y^2=-2zx\)
\(x^2+y^2-z^2=-2xy\)
➞ S = \(\dfrac{1}{-2xy}+\dfrac{1}{-2yz}+\dfrac{1}{-2zx}=\dfrac{x+y+z}{-2xyz}=0\)
Vậy S = 0
Cho x,y,z thỏa mãn: x,y,z khác 0 và x+y+z=0. Tính:
S=1/x^2+y^2-z^2 + 1/y^2+z^2-x^2 + 1/z^2+x^2-y^2
Ta có:
\(x+y+z=0\)
\(\Rightarrow\left(x+y\right)^2=\left(-z\right)^2\)
\(\Rightarrow x^2+y^2+2xy=z^2\)
\(\Rightarrow x^2+y^2-z^2=-2xy\)
Tương tự ta được:
\(S=\frac{1}{-2xy}+\frac{1}{-2yz}+\frac{1}{-2zx}=-\frac{1}{2}\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}\right)=-\frac{1}{2}\cdot\frac{x+y+z}{xyz}=0\)
Vậy S=0
Cho x,y,z >0. Chứng minh:
\(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\ge\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\)
Cho x,y,z thỏa mãn đk x/(y+z)+y/(x+z)+z/(x+y)=1
Tính giá trị của S=x^2/(y+z)+y^2/(x+z)+z^2/(x+y)
\(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1\Leftrightarrow\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}\right)=x+y+z\)
<=>\(\frac{x^2+x\left(y+z\right)}{y+z}+\frac{y^2+y\left(z+x\right)}{z+x}+\frac{z^2+z\left(x+y\right)}{x+y}=x+y+z\)
<=>\(\frac{x^2}{y+z}+x+\frac{y^2}{z+x}+y+\frac{z^2}{x+y}+z=x+y+z\)
<=>\(S=\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0\)
x/(y+z)+y/(x+z)+z/(x+y)=1
=>\(\frac{x^2}{\left(y+z\right)^2}\)+\(\frac{y^2}{\left(x+z\right)^2}\)+\(\frac{z^2}{\left(x+y\right)^2}\)+2(\(\frac{xy}{\left(y+z\right)\cdot\left(x+z\right)}\)+\(\frac{yz}{\left(x+z\right)\left(x+y\right)}\)+\(\frac{zx}{\left(z+y\right)\cdot\left(x+y\right)}\))=1
Cho x,y,z dương và x+y+z=1. Tìm Min của
S=x^2/y+z +y^2/z+x + z^2/x+y
Áp dụng bđt svacxo :
\(\frac{x^2}{x+y}+\frac{y^2}{y+z}+\frac{z^2}{z+x}\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{1}{2}\)
Dấu = xảy ra khi và chỉ khi \(x=y=z=\frac{1}{3}\)
Vậy \(Min_S=\frac{1}{2}\)khi \(x=y=z=\frac{1}{3}\)
Bài làm:
Áp dụng bất đẳng thức Svac-xơ ta có:
\(S=\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{1^2}{2.1}=\frac{1}{2}\)
Dấu "=" xảy ra khi: \(\frac{x}{y+z}=\frac{y}{x+z}=\frac{z}{y+x}\Rightarrow x=y=z=1\)
Vậy Min(S)=1 khi \(x=y=z=1\)
Học tốt!!!!
À mk nhầm dấu "=" xảy ra khi \(x=y=z=\frac{1}{3}\)nhé!
Bài 1: Cho x+y+z =0 và x^2+ y^2 + z^2=14
Tính S= x^4+y^4+z^4
Bài 2: Cho 1/x +1/y +1/z= 13 và x+y+z= xyz
Tính S= 1/x^2 +1/y^2 +1/z^2
Bài 3: Cho a,b,c khác 0 và a+b+c = 0
Tính S= 1/ a^2+b^2-c^2 + 1/b^2+c^2-a^2 +1/ c^2+a^2-b^2
Bài 4: Cho x>y>0 và 3x^2+ 3y^2 = 10xy
Tính S= x-y / x+y
Bài 5: Cho a^2+4b+4 và b^2+ 4c+4 và c^2+ 4a+4 = 0
Tính S= a^18+ b^18+ c^18
cho x2y-y2x-z2x+y2z+z2y=2xyz
c/m trong 3 số x,y,z có hai số bằng nhau hoặc đố nhau
Cho -1 _< x,y,z _< 2 và x+y+z=0. Tìm Max:
S=x^2+y^2+z^2
Ta có \(-1\le x,y,z\le2\Leftrightarrow\left(x+1\right)\left(x-2\right)\le0\Leftrightarrow x^2-x-2\le0\left(1\right)\)
Tương tự ta có: \(\hept{\begin{cases}y^2-y-2\le0\left(2\right)\\z^2-z-2\le0\left(3\right)\end{cases}}\)
Cộng từng vế (1)(2)(3) và do x+y+z=0 nên P\(\le6\left(4\right)\)
Từ hệ \(\hept{\begin{cases}\left(x+1\right)\left(x-2\right)=0\\\left(y+1\right)\left(y-2\right)=0\\\left(z+1\right)\left(z-2\right)=0\end{cases}}\)và x+y+z=2
=> trong 3 số x,y,z có một trong 2 số bằng 2 và hai số bằng -1
Vì thế chẳng hạn khi x=2; y=z=-1 (lúc đó x+y+z=0) ta có P=6
Vậy maxP=6
Cho -1 _< x,y,z _< 2 và x+y+z=3
Tìm Max S= x^2+y^2+z^2
Áp dụng bđt cauchy schwarz dạng engel ta có :
\(VP=\frac{x^2}{1}+\frac{y^2}{1}+\frac{z^2}{1}\le\frac{\left(x+y+z\right)^2}{3}=3\)
Dấu = xảy ra khi và chỉ khi \(x=y=z=1\)
Vậy \(Max_S=3\)khi \(x=y=z=1\)
Cho các số x, y, z dương. CMR:\(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\)\(\ge\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\)
Lời giải:
Xét hiệu:
\(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}-\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\right)=\frac{1}{2}\left[\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)+\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)-2\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\right)\right]\)
\(\ge \frac{1}{2}\left[\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)+3\sqrt[3]{\frac{x^2}{y^2}.\frac{y^2}{z^2}.\frac{z^2}{x^2}}-2\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\right)\right]\)
\(=\frac{1}{2}\left[\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)+3-2\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\right)\right]\)
\(=\frac{1}{2}\left[(\frac{x}{y}-1)^2+(\frac{y}{z}-1)^2+(\frac{z}{x}-1)^2\right]\geq 0\)
\(\Rightarrow \frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\geq \frac{x}{y}+\frac{y}{z}+\frac{z}{x}\) (đpcm)
Dấu "=" xảy ra khi $x=y=z$